Introduction
This post was inspired from a challenge on Cyber Apocalypse 2021, Alien Camp. In this challenge you were given a series of linear equations that consist of emojis, and your task was to solve 500 of those equations correctly in a small time period. In the challenge you could just ask for the emoji translation and the remote server responded with the emoji’s value. But what if this help was not given? That is what is happening in this challenge.
Matrix Basics
If any of the linear algebra terms used below seem unfamiliar or you need a refresher on them, read my Matrix Algebra Basics post.
Initial Assessment
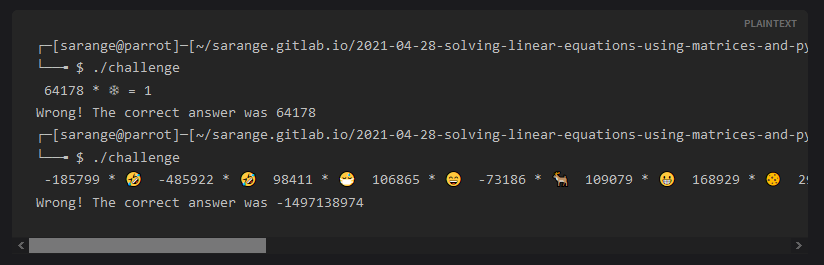
By running the executable we see that a random equation appears, with random number of emojis and random multipliers.
1
2
3
4
5
6
7
8
┌─[sarange@parrot]─[~/sarange.gitlab.io/2021-04-28-solving-linear-equations-using-matrices-and-python]
└──╼ $ ./challenge
64178 * ❄ = 1
Wrong! The correct answer was 64178
┌─[sarange@parrot]─[~/sarange.gitlab.io/2021-04-28-solving-linear-equations-using-matrices-and-python]
└──╼ $ ./challenge 1 ↵
-185799 * 🤣 -485922 * 🤣 98411 * 😷 106865 * 😄 -73186 * 🦌 109079 * 😀 168929 * 🍪 296146 * 🧝 = 1
Wrong! The correct answer was -1497138974
Basic Idea
Based on the description of the challenge, the objective is to find the kernel of the linear map that is produced by the linearly independent matrix of the multiple equations.
Helper Functions
We will use pwntools and the following helpers so that we can make our life easier.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from pwn import *
from re import findall
import numpy as np
name = './challenge'
# Get a new pwntools process
def get_connection():
p = process(name)
logging.info('Process created')
return p
# Send the answer provided to the process p and return the received the response
def send_answer(p, answer):
p.sendline(answer)
p.recvuntil('\n')
response = p.recvuntil('\n')
wrong = findall(br'answer was (-?\d+)\n', response)
if len(wrong) == 1:
return int(wrong[0])
else:
return 'Correct!'
# Parse the process response to a tuple of (multiplier, emoji)
def get_equation(p):
try:
question = p.recvuntil('=')
except EOFError:
print(p.recvall(0.1).decode('utf-8'))
return None
equation_pair = findall(br'(-?\d+)\s\*\s([^\s]+)\s', question)
return equation_pair
# Get a vector the multipliers of the equation_pair using the emoji_list as index
def vector_from_equation_pair(emoji_list, equation_pair):
vector = np.array([0] * len(emoji_list))
for number, emoji in equation_pair:
vector[emoji_list.index(emoji)] = int(number)
return vector
Finding the variables
We can start by collecting all the emojis that appear in the equations. By knowing that, we can know the amount of columns that our final matrix will have. For that reason, we create the function get_all_emojis that takes as an argument the amount of equations to receive from the executable and return to us them in a set (unique entries).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Get num amount of connections and send wrong answers to that we can gather the
# amount of emojis used
def get_all_emojis(num):
emojis = set()
for _ in range(num):
p = get_connection()
equation_pair = get_equation(p)
emoji = [e[1] for e in equation_pair]
emojis.update(emoji)
p.close()
return list(emojis)
if __name__ == '__main__':
print(get_all_emojis(50))
Finding the matrix
Now we have to get the same amount of linearly independent rows as columns, let’s say \(n\). By getting \(n\) equations we may get linearly dependent equations that will not contribute to the rank of our matrix. We need the matrix to be a full rank matrix so that the kernel space will be of dimension 1. So we set a matrix matrix_A with 1 line of zeros and \(n\) columns and a matrix matrix_B as a vector matrix of 1 row of zero. Then we loop until the rank of matrix_A is \(n\) and do the following:
- Get a new connection
- Get the equations presented and parse it
- Add it to
new_matrix_A, a temporary copy ofmatrix_A - Send a wrong answer and get the correct one in response
- Add it to
new_matrix_B, a temporary copy ofmatrix_B - If the rank of
new_matrix_Ais bigger than the rank ofmatrix_A, make thematrix_Aequal thenew_matrix_A
When the rank of the matrix matrix_A is \(n\) we can use numpy to solve the equation \(\pmb{A} \cdot \mathscr{X} = \pmb{B}\).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Get as many equations as to get a full rank matrix and then solve the equations AX=B
# with numpy, return the resulting vector matrix
def solve(emoji_list):
target_rank = len(emoji_list)
matrix_A = Matrix([[0] * target_rank])
matrix_B = Matrix([[0]])
while not matrix_A.rank() == target_rank:
p = get_connection()
equation_pair = get_equation(p)
vector = vector_from_equation_pair(emoji_list, equation_pair)
new_matrix_A = matrix_A.row_insert(0, Matrix([vector]))
response = send_answer(p, '1337')
new_matrix_B = matrix_B.row_insert(0, Matrix([response]))
if new_matrix_A.rank() > matrix_A.rank():
matrix_A = new_matrix_A
matrix_B = new_matrix_B
p.close()
matrix_A.row_del(len(emoji_list))
matrix_B.row_del(len(emoji_list))
matrix_A = np.array(matrix_A, dtype='float64')
matrix_B = np.array(matrix_B, dtype='float64')
solution = np.linalg.solve(matrix_A, matrix_B)
return solution
Get the flag
Now that we have the solution matrix, the only ting that we need to do is get the equations presented, parse them, multiply the solution matrix with them and send the answers until we get the flag.
Solver
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
from pwn import *
from re import findall
from sympy import Matrix
import numpy as np
import _pickle as cPickle
name = './challenge'
context.log_level = 'critical'
# Get a new pwntools process
def get_connection():
p = process(name)
logging.info('Process created')
return p
# Parse the process response to a tuple of (multiplier, emoji)
def get_equation(p):
try:
question = p.recvuntil('=')
except EOFError:
print(p.recvall(0.1).decode('utf-8'))
return None
equation_pair = findall(br'(-?\d+)\s\*\s([^\s]+)\s', question)
return equation_pair
# Send the answer provided to the process p and return the received the response
def send_answer(p, answer):
p.sendline(answer)
p.recvuntil('\n')
response = p.recvuntil('\n')
wrong = findall(br'answer was (-?\d+)\n', response)
if len(wrong) == 1:
return int(wrong[0])
else:
return 'Correct!'
# Get a vector the multipliers of the equation_pair using the emoji_list as index
def vector_from_equation_pair(emoji_list, equation_pair):
vector = np.array([0] * len(emoji_list))
for number, emoji in equation_pair:
vector[emoji_list.index(emoji)] = int(number)
return vector
# Get num amount of connections and send wrong answers to that we can gather the
# amount of emojis used
def get_all_emojis(num):
emojis = set()
for _ in range(num):
p = get_connection()
equation_pair = get_equation(p)
emoji = [e[1] for e in equation_pair]
emojis.update(emoji)
p.close()
return list(emojis)
# Get as many equations as to get a full rank matrix and then solve the equations
# AX=B with numpy, return the resulting
# vector matrix
def solve(emoji_list):
target_rank = len(emoji_list)
matrix_A = Matrix([[0] * target_rank])
matrix_B = Matrix([[0]])
while not matrix_A.rank() == target_rank:
p = get_connection()
equation_pair = get_equation(p)
vector = vector_from_equation_pair(emoji_list, equation_pair)
new_matrix_A = matrix_A.row_insert(0, Matrix([vector]))
response = send_answer(p, '1337')
new_matrix_B = matrix_B.row_insert(0, Matrix([response]))
if new_matrix_A.rank() > matrix_A.rank():
matrix_A = new_matrix_A
matrix_B = new_matrix_B
p.close()
matrix_A.row_del(len(emoji_list))
matrix_B.row_del(len(emoji_list))
matrix_A = np.array(matrix_A, dtype='float64')
matrix_B = np.array(matrix_B, dtype='float64')
solution = np.linalg.solve(matrix_A, matrix_B)
return solution
if __name__ == '__main__':
# If already saved, get the saved list, else get the list and save it
try:
with open('emoji_list.pkl', 'rb') as f:
emoji_list = cPickle.load(f)
except FileNotFoundError:
emoji_list = get_all_emojis(50)
with open('emoji_list.pkl', 'wb') as f:
cPickle.dump(emoji_list, f)
# If already saved, get the saved vector matrix, else get the vector matrix and
# save it
try:
with open('emoji_matrix.pkl', 'rb') as f:
emoji_matrix = cPickle.load(f)
except FileNotFoundError:
emoji_matrix = [np.round(emoji_value) for emoji_value in solve(emoji_list)]
with open('emoji_matrix.pkl', 'wb') as f:
cPickle.dump(emoji_matrix, f)
# Finally solve the equations using the matrix from above until the equation_pair
# is None
p = get_connection()
while True:
equation_pair = get_equation(p)
if equation_pair is None:
exit()
vector = vector_from_equation_pair(emoji_list, equation_pair)
answer = int(np.matmul(np.array([vector]), emoji_matrix))
response = send_answer(p, str(answer))