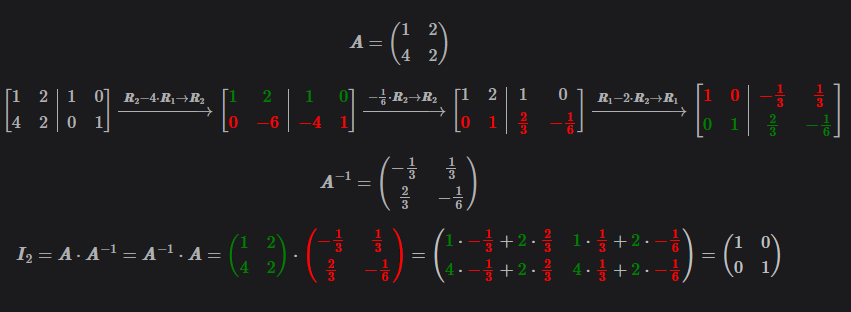
What is a Matrix
A matrix \(\pmb{A} \in \mathbb{N}^{m \times n}\) is an array of elements of a field \(\{ k \in \mathbb{K}^{m \times n} | m,n \in \mathbb{N} \}\), \(m\) being the rows and \(n\) being the columns of the matrix.
Example: A matrix \(\pmb{A} = \begin{pmatrix} 0 & 1 & -1\\ 3 & -9 & 0 \end{pmatrix} \in \mathbb{N}^{2 \times 3}\) is similar to a C array
1
2
3
4
5
int [2][3] =
{
{0, 1, -1},
{3, -9, 0}
}
Matrix Operations
There are 3 operations between matrices:
- Scalar multiplication:
Exapmle: \(7 \cdot \begin{pmatrix} 1 & -2 & 3 \\ 4 & 2 & 0 \end{pmatrix} = \begin{pmatrix} 7 & -14 & 21 \\ 28 & 14 & 0 \end{pmatrix}\)
- Matrix addition (only possible between matrices of the same dimensions):
Exapmle: \(\begin{pmatrix} 1 & -2 & 3 \\ 4 & 2 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 2 & -9 \\ 4 & 1 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 & -6 \\ 8 & 3 & 3 \end{pmatrix}\)
- Matrix multiplication (only possible between a matrix \(A_{m,n}\) and a matrix \(B_{n,q}\)):
or for \(c_{i,j} \in \pmb{C} = \pmb{A} \cdot \pmb{B}\), we have
\[c_{i,j} = \sum_{k=1}^n a_{i,k} b_{k,j}\]Exapmle: \(\begin{pmatrix} 1 & -2 & 3 \\ 4 & 2 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 2 \\ 4 & 1 \\ 1 & 3 \end{pmatrix} = \begin{pmatrix} 1 \cdot 0-2 \cdot 4+3 \cdot 1 & 1 \cdot 2-2 \cdot 1+3 \cdot 3\\ 4 \cdot 0+2 \cdot 4+0 \cdot 1 & 4 \cdot 2+2 \cdot 1+0 \cdot 3 \end{pmatrix} = \begin{pmatrix} -5 & 9\\ 8 & 10 \end{pmatrix}\)
Note that matrix multiplication is not a commutative operation, meaning that \(\pmb{A} \cdot \pmb{B} \neq \pmb{B} \cdot \pmb{A}\).
Vector Operations
By addressing a vector, we refer to either rows or columns of a matrix. There are three vector operations, let’s denote the \(n\)-th row as \(\pmb{R}_n\):
- Vector addition, where \(i \neq j\):
or
\[\pmb{R}_j + \pmb{R}_i \rightarrow \pmb{R}_i\]Exapmle: (\(\pmb{R}_1 + \pmb{R}_2 \rightarrow \pmb{R}_2\)): \(\begin{pmatrix} \color{green} 1 & \color{green} -2 & \color{green}3 \\ \color{red}4 & \color{red}2 & \color{red}0 \\ 6 & 8 & 0 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & -2 & 3 \\ \color{red} 4 \color{silver} + \color{green} 1 & \color{red} 2 \color{silver} - \color{green} 2 & \color{red} 0 \color{silver} + \color{green} 3 \\ 6 & 8 & 0 \end{pmatrix} = \begin{pmatrix} 1 & -2 & 3 \\ 5 & 0 & 3 \\ 6 & 8 & 0 \end{pmatrix}\)
- Vector multiplication, where scalar \(\lambda \neq 0\):
or
\[\lambda \cdot \pmb{R}_i \rightarrow \pmb{R}_i\]Exapmle: (\(3 \cdot \pmb{R}_2 \rightarrow \pmb{R}_2\)): \(\begin{pmatrix} 1 & -2 & 3 \\ \color{green} 4 & \color{green} 2 & \color{green} 0 \\ 6 & 8 & 0 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & -2 & 3 \\ \color{red} 3 \color{silver} \cdot \color{green} 4 & \color{red} 3 \color{silver} \cdot \color{green} 2 & \color{red} 3 \color{silver} \cdot \color{green} 0 \\ 6 & 8 & 0 \end{pmatrix} = \begin{pmatrix} 1 & -2 & 3 \\ 12 & 6 & 0 \\ 6 & 8 & 0 \end{pmatrix}\)
- Vector switching:
or
\[\pmb{R}_i \leftrightarrow \pmb{R}_j\]Exapmle: (\(\pmb{R}_1 \rightarrow \pmb{R}_2\)): \(\begin{pmatrix} \color{red} 1 & \color{red} -2 & \color{red} 3 \\ \color{green} 4 & \color{green} 2 & \color{green} 0 \\ 6 & 8 & 0 \end{pmatrix} \rightarrow \begin{pmatrix} \color{green} 4 & \color{green} 2 & \color{green} 0 \\ \color{red} 1 & \color{red} -2 & \color{red} 3 \\ 6 & 8 & 0 \end{pmatrix}\)
These operations can be performed to rows or columns and are refer to as row operations and column operations respectively.
Linear Independence
A matrix is linearly dependent if at least one of it’s vectors (rows/columns) can be defined as a linear combination of the others.
Example:
\[\pmb{A} = \begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix} \rightarrow \pmb{R}_2 = 2 \cdot \pmb{R}_1 \rightarrow \pmb{A} \text{ linearly dependent}\]If a matrix is not linearly dependent, it is linearly independent.
This means that if every row of the matrix cannot be defined as a linear combination of the other vectors.
A linearly independent matrix can only be square and it is equivalent (row/column equivalent) with the identity matrix.
Example:
\[\pmb{R}_2 - 4 \cdot \pmb{R}_1 \rightarrow \pmb{R}_2\] \[\pmb{R}_3 - 6 \cdot \pmb{R}_1 \rightarrow \pmb{R}_3\] \[\pmb{R}_3 - 2 \cdot \pmb{R}_2 \rightarrow \pmb{R}_3\] \[\frac{1}{6} \cdot \pmb{R}_3 \rightarrow \pmb{R}_3\] \[\pmb{R}_2 + 12 \cdot \pmb{R}_3 \rightarrow \pmb{R}_2\] \[\frac{1}{10} \cdot \pmb{R}_2 \rightarrow \pmb{R}_2\] \[\pmb{R}_1 -3 \cdot \pmb{R}_3 \rightarrow \pmb{R}_1\] \[\pmb{R}_1 + 2 \cdot \pmb{R}_2 \rightarrow \pmb{R}_1\]or
\[\begin{pmatrix} 1 & -2 & 3 \\ 4 & 2 & 0 \\ 6 & 8 & 0 \end{pmatrix} \xrightarrow{\pmb{R}_2 - 4 \cdot \pmb{R}_1 \rightarrow \pmb{R}_2} \begin{pmatrix} \color{green} 1 & \color{green} -2 & \color{green} 3 \\ \color{red} 0 & \color{red} 10 & \color{red} -12 \\ 6 & 8 & 0 \end{pmatrix} \xrightarrow{\pmb{R}_3 - 6 \cdot \pmb{R}_1 \rightarrow \pmb{R}_3} \begin{pmatrix} \color{green} 1 & \color{green} -2 & \color{green} 3 \\ 0 & 10 & -12 \\ \color{red} 0 & \color{red} 20 & \color{red} -18 \end{pmatrix} \xrightarrow{\pmb{R}_3 - 2 \cdot \pmb{R}_2 \rightarrow \pmb{R}_3}\] \[\begin{pmatrix} 1 & -2 & 3 \\ \color{green} 0 & \color{green} 10 & \color{green} -12 \\ \color{red} 0 & \color{red} 0 & \color{red} 6 \end{pmatrix} \xrightarrow{\frac{1}{6} \cdot \pmb{R}_3 \rightarrow \pmb{R}_3} \begin{pmatrix} 1 & -2 & 3 \\ 0 & 10 & -12 \\ \color{red} 0 & \color{red} 0 & \color{red} 1 \end{pmatrix} \xrightarrow{\pmb{R}_2 + 12 \cdot \pmb{R}_3 \rightarrow \pmb{R}_2} \begin{pmatrix} 1 & -2 & 3 \\ \color{red} 0 & \color{red} 10 & \color{red} 0 \\ \color{green} 0 & \color{green} 0 & \color{green} 1 \end{pmatrix} \xrightarrow{\frac{1}{10} \cdot \pmb{R}_2 \rightarrow \pmb{R}_2}\] \[\begin{pmatrix} 1 & -2 & 3 \\ \color{red} 0 & \color{red} 1 & \color{red} 0 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{\pmb{R}_1 -3 \cdot \pmb{R}_3 \rightarrow \pmb{R}_1} \begin{pmatrix} \color{red} 1 & \color{red} -2 & \color{red} 0 \\ 0 & 1 & 0 \\ \color{green} 0 & \color{green} 0 & \color{green} 1 \end{pmatrix} \xrightarrow{\pmb{R}_1 + 2 \cdot \pmb{R}_2 \rightarrow \pmb{R}_1} \begin{pmatrix} \color{red} 1 & \color{red} 0 & \color{red} 0 \\ \color{green} 0 & \color{green} 1 & \color{green} 0 \\ 0 & 0 & 1 \end{pmatrix} = \pmb{I}_3\]Transpose Matrix
The transpose \(\pmb{A}^T\) of a matrix \(\pmb{A}\) is a matrix which is flipped over its diagonal, or in other words, it has it’s rows and columns switched from the matrix \(\pmb{A}\).
Matrix Ranks
The rank of a matrix \(\pmb{A}\) is the dimension of the vector space spanned by its columns, or in other words, the maximal number of linearly independent vector of the matrix \(\pmb{A}\), as a consequence, the rank of a matrix cannot be greater than it’s smallest dimension, \(\{\pmb{A} \in \mathbb{K}^{m \times n}, m < n\} \Rightarrow Rank(\pmb{A}) \leq m\).
The rank of a matrix is the same as it’s transpose, as it’s linearly independent vectors are the same in count, \(Rank(\pmb{A})=Rank(\pmb{A}^T)\).
If a matrix is square and it’s vectors are linearly independent, then this matrix is called a full rank matrix, \(\{\pmb{A} \in \mathbb{K}^{n \times n}, \pmb{A} \text{ is linearly independent}\} \Rightarrow Rank(\pmb{A}) = n\).
Determinant of a Matrix
The determinant is a scalar value characterizing the entries of a square matrix. The determinant is nonzero if and only if the matrix is a full rank matrix. It can be represented as \(det(\pmb{A})\) or \(|\pmb{A}|\).
- $ det(\lambda \cdot \pmb{A}) = \lambda \cdot det(\pmb{A}) $
- $ det(\pmb{A}) = det(\pmb{A}^T) $
- $ det(\pmb{I}) = 1 $
The determinant of a \(2 \times 2\) matrix can be calculated with the following formula:
\[det \left( \begin{pmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{pmatrix} \right) = a_{1,1} \cdot a_{2,2} - a_{1,2} \cdot a_{2,1}\]The determinant of bigger matrices can be found by reducing the matrix to a \(2 \times 2\) matrix like the \(3 \times 3\) example below:
\[det \left( \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \end{pmatrix} \right) =\] \[a_{1,1} \cdot det \left( \begin{pmatrix} a_{2,2} & a_{2,3} \\ a_{3,2} & a_{3,3} \end{pmatrix} \right) - a_{2,1} \cdot det \left( \begin{pmatrix} a_{1,2} & a_{1,3} \\ a_{3,2} & a_{3,3} \end{pmatrix} \right) + a_{3,1} \cdot det \left( \begin{pmatrix} a_{1,2} & a_{1,3} \\ a_{2,2} & a_{2,3} \end{pmatrix} \right) =\] \[a_{1,1} \cdot a_{2,2} \cdot a_{3,3} - a_{1,1} \cdot a_{2,3} \cdot a_{3,2} a_{2,1} \cdot a_{1,2} \cdot a_{3,3} - a_{2,1} \cdot a_{1,3} \cdot a_{3,2} a_{3,1} \cdot a_{1,2} \cdot a_{2,3} - a_{3,1} \cdot a_{1,3} \cdot a_{2,2}\]Linear Transformations
A linear transformation \(\mathscr{L}: \mathcal{V} \rightarrow \mathcal{W}\) is a mapping \(\mathcal{V} \rightarrow \mathcal{W}\) between two vector spaces that preserves the operations of vector addition and scalar multiplication. Let \(u,v \in \mathcal{V}\) and a scalar \(\lambda \in \mathbb{K}\), then \(\mathscr{L}: \mathcal{V} \rightarrow \mathcal{W}\) is a linear transformation if and only if:
\[\begin{matrix} \mathscr{L}(u + v) = \mathscr{L}(u) + \mathscr{L}(v) \\ \mathscr{L}(\lambda \cdot v) = \lambda \cdot \mathscr{L}(v) \end{matrix}\]Kernel Space
Kernel space is the linear subspace of the domain of a map which is mapped to the zero vector. That is, given a linear map \(\mathscr{L} : \mathcal{V} \rightarrow \mathcal{W}\) between two vector spaces \(\mathcal{V}\) and \(\mathcal{W}\), the kernel of \(\mathscr{L}\) is the vector space of all elements \(v \in \mathcal{V}\) such that \(\mathscr{L}(v) = 0\), where 0 denotes the zero vector in \(\mathcal{W}\)
\[ker(\mathscr{L}) = \{ v \in \mathcal{V} | \mathscr{L}(v) = 0_{\mathcal{W}} \}\]Consider that a matrix \(\pmb{A} \in \mathbb{K}^{\mathcal{V} \times \mathcal{W}}\) is nothing more than a linear transformation that maps elements from \(\mathbb{K}^{\mathcal{V}}\) to \(\mathbb{K}^{\mathcal{W}}\). This in turn means that for \(\pmb{A} \in \mathbb{K}^{m \times n}, \mathscr{X} \in \mathbb{K}^{n \times 1}\) and \(\pmb{0}_m\) as the \(m\)-dimensional zero vector, then the kernel space of the linear transformation \(\mathscr{L}(\mathscr{X}) = \pmb{A} \cdot \mathscr{X}, \mathscr{X} \in \mathbb{K}^{n \times 1}\) is the space of answers to the linear equation \(\pmb{A} \cdot \mathscr{X} = \pmb{0}_m\)
Inverse Matrix
The inverse matrix \(\pmb{A}^{-1}\) of a matrix \(\pmb{A}\) is a matrix that when multiplied with the matrix \(\pmb{A}\) we get the identity matrix \(\pmb{I}_n = \pmb{A} \cdot \pmb{A}^{-1} = \pmb{A}^{-1} \cdot \pmb{A} = \pmb{A}^{-1} \cdot (\pmb{A}^{-1})^{-1}\). Not all have an inverse, for a matrix to have an inverse, it need to be a full rank matrix.
A matrix that can be transformed to the identity matrix \(\mathbb{I}_n\) with a series of vector operations, the inverse matrix of it can be found by performing the same series of operations to the identity matrix \(\mathbb{I}_n\).
Example:
\[\pmb{A} = \begin{pmatrix} 1 & 2 \\ 4 & 2 \end{pmatrix}\] \[\left[ \begin{array}{cc|cc} 1 & 2 & 1 & 0\\ 4 & 2 & 0 & 1 \end{array} \right] \xrightarrow{\pmb{R}_2 - 4 \cdot \pmb{R}_1 \rightarrow \pmb{R}_2} \left[ \begin{array}{cc|cc} \color{green} 1 & \color{green} 2 & \color{green} 1 & \color{green} 0\\ \color{red} 0 & \color{red} -6 & \color{red} -4 & \color{red} 1 \end{array} \right] \xrightarrow{-\frac{1}{6} \cdot \pmb{R}_2 \rightarrow \pmb{R}_2} \left[ \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\ \color{red} 0 & \color{red} 1 & \color{red} \frac{2}{3} & \color{red} - \frac{1}{6} \end{array} \right] \xrightarrow{\pmb{R}_1 - 2 \cdot \pmb{R}_2 \rightarrow \pmb{R}_1} \left[ \begin{array}{cc|cc} \color{red} 1 & \color{red} 0 & \color{red} - \frac{1}{3} & \color{red} \frac{1}{3}\\ \color{green} 0 & \color{green} 1 & \color{green} \frac{2}{3} & \color{green} - \frac{1}{6} \end{array} \right]\] \[\pmb{A}^{-1} = \begin{pmatrix} - \frac{1}{3} & \frac{1}{3} \\ \frac{2}{3} & - \frac{1}{6} \end{pmatrix}\] \[\pmb{I}_2 = \pmb{A} \cdot \pmb{A}^{-1} = \pmb{A}^{-1} \cdot \pmb{A} = \color{green} \begin{pmatrix} 1 & 2 \\ 4 & 2 \end{pmatrix} \color{silver} \cdot \color{red} \begin{pmatrix} - \frac{1}{3} & \frac{1}{3} \\ \frac{2}{3} & - \frac{1}{6} \end{pmatrix} \color{silver} = \begin{pmatrix} \color{green} 1 \color{silver} \cdot \color{red} - \frac{1}{3} \color{silver} + \color{green} 2 \color{silver} \cdot \color{red} \frac{2}{3} & \color{green} 1 \color{silver} \cdot \color{red} \frac{1}{3} \color{silver} + \color{green} 2 \color{silver} \cdot \color{red} - \frac{1}{6} \\ \color{green} 4 \color{silver} \cdot \color{red} - \frac{1}{3} \color{silver} + \color{green} 2 \color{silver} \cdot \color{red} \frac{2}{3} & \color{green} 4 \color{silver} \cdot \color{red} \frac{1}{3} \color{silver} + \color{green} 2 \color{silver} \cdot \color{red} - \frac{1}{6} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\]Linear Equations to Matrices
Let’s say we have a set of linear equations:
\[\begin{matrix} a_{1,1}x_1 + a_{1,2}x_2 + \cdots + a_{1,m}x_m = b_1, \\ a_{2,1}x_1 + a_{2,2}x_2 + \cdots + a_{2,m}x_m = b_2, \\ \vdots \\ a_{n,1}x_1 + a_{n,2}x_2 + \cdots + a_{n,m}x_m = b_n \\ \end{matrix}\]and we want to represent it with matrices like \(\pmb{A}_{m, n} \cdot \mathscr{X}_{m, 1} = \pmb{B}_{n, 1}\), with \(\pmb{A} \in \mathbb{K}^{m \times n}, \mathscr{X} \in \mathbb{K}^m, \pmb{C} \in \mathbb{K}^n\). The steps that we need to follow are:
- Put the scalars \(a_{1,1}, a_{1,2}, \cdots, a_{n,m}\) of the variables in a \(m \times n\) matrix \(\pmb{A}\).
- Put the variables \(x_1, x_2, \cdots, x_m\) of the variables in a \(m \times 1\) matrix \(\mathscr{X}\).
- Put the results of the equations \(c_1, c_2, \cdots, c_n\) of the variables in a \(n \times 1\) matrix \(\pmb{B}\).
So we will end up with the following matrix equation:
\[\begin{pmatrix} a_{1,1} + a_{1,2} + \cdots + a_{1,m} \\ a_{2,1} + a_{2,2} + \cdots + a_{2,m} \\ \vdots \\ a_{n,1} + a_{n,2} + \cdots + a_{n,m} \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \\ \end{pmatrix} = \begin{pmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \\ \end{pmatrix}\]Let’s assume that the the equations are linearly independent, or, the matrix \(\pmb{A}\) is linearly independent. Then, we can conclude that for \(\mathscr{K}\) being the kernel space of \(\pmb{A}\):
If \(m > n\), meaning the equations are less than the variables, the rank of the answer space will be \(Rank(\mathscr{K}) = m - n\) or \(\mathscr{K} \subseteq \mathbb{K}^{m - n}\).
If \(m < n\), meaning the equations are more than the variables, the rank of the answer space will be \(Rank(\mathscr{K}) = 0\) or \(\mathscr{K} \subseteq \emptyset\).
If \(m = n\), meaning the equations are equal with the variables, the rank of the answer space will be \(Rank(\mathscr{K}) = 1\) or \(\mathscr{K} \subseteq \mathbb{K}\).
Example 1:
Let’s say we have the following equations and we need to solve for $ x,y $ and $ z $:
\[\begin{cases} 3x + 2y = 9 \\ x - z = -2 \\ y + 2z = 0 \end{cases}\]We can build the matrices \(\pmb{A}, \mathscr{X}\) and \(\pmb{B}\):
\[\pmb{A} = \begin{pmatrix} 3 & 2 & 0 \\ 1 & 0 & -1 \\ 0 & 1 & 2 \end{pmatrix}, \mathscr{X} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}, \pmb{B} = \begin{pmatrix} 9 \\ -2 \\ 0 \end{pmatrix}\]Then we have:
\[\pmb{A} \cdot \mathscr{X} = \pmb{B} \Rightarrow \pmb{A}^{-1} \cdot \pmb{A} \cdot \mathscr{X} = \pmb{A}^{-1} \cdot \pmb{B} \Rightarrow \mathscr{X} = \pmb{A}^{-1} \cdot \pmb{B}\]With the method mentioned here we find the inverse matrix \(\pmb{A}^{-1}\) of matrix \(\pmb{A}\):
\[\pmb{A}^{-1} = \begin{pmatrix} -1 & 4 & 2 \\ 2 & -6 & -3 \\ -1 & 3 & 2 \\ \end{pmatrix} \Rightarrow \mathscr{X} = \pmb{A}^{-1} \cdot \pmb{B} = \begin{pmatrix} -1 & 4 & 2 \\ 2 & -6 & -3 \\ -1 & 3 & 2 \\ \end{pmatrix} \cdot \begin{pmatrix} 9 \\ -2 \\ 0 \end{pmatrix} = \begin{pmatrix} -17 \\ 30 \\ -15 \end{pmatrix}\]Example 2:
Let’s say we have the following equations and we need to solve for $ x,y $ and $ z $:
\[\begin{cases} 3x + 2y = 9 \\ x - z = -2 \\ 2x + 2y + z = 11 \end{cases}\]We can transform the matrices \(\pmb{A}\) and \(\pmb{B}\) together with vector operations:
\[\pmb{A} = \left( \begin{array}{ccc|c} 3 & 2 & 0 & 9 \\ 1 & 0 & -1 & -2 \\ 2 & 2 & 1 & 11 \end{array} \right) \rightarrow \left( \begin{array}{ccc|c} \color{red} 2 & \color{red} 2 & \color{red} 1 & \color{red} 11 \\ \color{green} 1 & \color{green} 0 & \color{green} -1 & \color{green} -2 \\ 2 & 2 & 1 & 11 \end{array} \right) \rightarrow \left( \begin{array}{ccc|c} \color{green} 2 & \color{green} 2 & \color{green} 1 & \color{green} 11 \\ 1 & 0 & -1 & -2 \\ \color{red} 0 & \color{red} 0 & \color{red} 0 & \color{red} 0 \end{array} \right) \rightarrow\] \[\left( \begin{array}{ccc|c} \color{red} 0 & \color{red} 2 & \color{red} -2 & \color{red} 15 \\ \color{green} 1 & \color{green} 0 & \color{green} -1 & \color{green} -2 \\ 0 & 0 & 0 & 0 \end{array} \right) \rightarrow \left( \begin{array}{ccc|c} 1 & 0 & -1 & -2 \\ \color{red} 0 & \color{red} 1 & \color{red} -1 & \color{red} \frac{15}{2} \\ 0 & 0 & 0 & 0 \end{array} \right)\]As we see the matrix \(\pmb{A}\) is linearly dependant and the rank of the matrix \(\pmb{A}\) is the number of it’s linearly independent rows \(Rank(\pmb{A}) = 2\), so the kernel space of the vector-matrix \(\mathscr{X}\) is a \(1\)-dimensional subspace \(ker(\mathscr{X}) \subseteq \mathbb{R}\).
\[\begin{cases} x = z -2 \\ y = z + \frac{15}{2} \\ z \in \mathbb{R} \end{cases}\]